
Dat de sterren niet allemaal even helder zijn, valt zelfs de meest oppervlakkige waarnemer op. Het is waarschijnlijk de Griekse astronoom Hipparchus van Nicaea (190 - 120 v.C.) die voor het eerst een systematische indeling van de sterren volgens helderheidsklassen publiceerde.
Hipparchus onderscheidde zes grootteklassen. Sterren van de eerste grootte zijn het helderst: Wega, Deneb, Rigel,... Daarna komen de steren van de tweede grootte, bijvoorbeeld de Poolster, en zo verder tot bij de sterren die nog maar net met het blote oog zichtbaar zijn, de zesde grootteklasse.

De helderheidsgrootte van een ster wordt meestal met het uit het Latijns afkomstige woord magnitude aangeduid.
In 1869 ontdekten Ernst Weber en Gustav Fechner dat veranderingen van zintuiglijke prikkels niet in constante stappen worden waargenomen, maar in verhoudingen. Zo luidt de wet van Weber:
Het nog net waarneembare verschil is een constant gedeelte van de intensiteit van de stimulus.
Deze wet is van toepassing op alle soorten zintuiglijke gewaarwordingen: helderheid van licht, geluidssterkte, toonhoogte, gewichten torsen, zoute smaak, geur van rubber,...
Een gevolg hiervan is dat wanneer wetenschappers een meetschaal uitvinden die zuiver empirisch is (d.i. op waarneming gebaseerd), deze schaal een logartimisch karakter vertoont. Dat wil zeggen dat verschillen op de schaal overeenkomen met verhoudingen in de realiteit.
Toonladders zijn logaritmisch: een octaaf komt altijd overeen met een frequentieverhouding van 1 op 2, of je nu helemaal links dan wel helemaal rechts op het toetsenbord van de piano zit. En ook de decibelschaal is een logaritmische schaal: 10 decibel komt overeen met een verhouding van 1 op 10 in geluidssterkte.
De magnitudenschaal van de oude Grieken bleek achteraf logaritmisch te zijn: de helderheidsverhouding tussen sterren van magnitude 1 en 2 is ongeveer gelijk aan de helderheidsverhouding tussen sterren van magnitude 5 en 6.
De grootte van de helderheidsverhouding tussen sterren van opeenvolgende magnituden wordt bepaald door de vaststelling dat sterren van magnitude 1 ongeveer 100 keer zo helder zijn als sterren van magnitude 6.
Hoeveel is nu de helderheidsverhouding die overeenkomt met één magnitudeverschil ? Daarvoor moeten we een getal a vinden met de volgende eigenschappen:
Een ster van magnitude 1 is a keer helderder dan een ster van magnitude 2.
Een ster van magnitude 2 is a keer helderder dan een ster van magnitude 3.
Een ster van magnitude 3 is a keer helderder dan een ster van magnitude 4.
Een ster van magnitude 4 is a keer helderder dan een ster van magnitude 5.
Een ster van magnitude 5 is a keer helderder dan een ster van magnitude 6.
Samengesteld geeft dit: a x a x a x a x a = 100. Dus
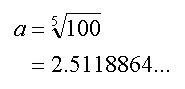
Sinds het gebruik van de telescoop zijn natuurlijk sterren waargenomen die veel zwakker zijn dan magnitude 6. Daartoe is de magnitudenschaal dan gewoon logaritmisch uitgebreid met de getallen 7, 8,... De zwakste objecten die met de vijfmetertelescoop van Mount Palomar kunnen worden gefotografeerd, hebben magnitude 23. Met de Faint Object Camera van de Hubble Space Telescope geraken we aan magnitude 27.
Aan de andere kant van de schaal is een uitbreiding mogelijk naar heldere objecten; Zo zijn sommige sterren die door de Grieken in de eerste klasse waren geplaatst, eigenlijk een beetje te helder. Wega heeft magnitude 0. De planeet Venus heeft magnitude -4. De volle Maan krijgt -13, en de Zon -27.
Onderstaande tabel geeft in enkele van deze gevallen de overeenkomstige helderheidsverhouding, telkens in vergelijking met een ster van magnitude 0. De laatste rij van de tabel fungeert als een eenvoudige magnituden-rekenmachine: vul in het linker blanco tekstveld een magnitudenverschil in, en druk op de bovenste van de twee knoppen (gemarkeerd ">>>"). Of vul in het rechter tekstveld een helderheidsverhouding in, en druk op de onderste van de twee knoppen (gemarkeerd "<<<"). Let erop dat gebroken getallen met een punt (.) getypt worden, niet met een komma.
| magnitude | verhouding |
|---|---|
| 0 | 1 |
| 1 | 2.51 |
| 2 | 6.31 |
| 3 | 15.8 |
| 4 | 39.8 |
| 5 | 100 |
| 6 | 251 |
| 23 | 1 584 893 192 |
| 27 | 63 095 734 448 |
| -4 | 1/40 |
| -13 | 1/158000 |
| -27 | 1/63 miljard |
Ook gebroken magnituden zijn mogelijk. Een ster van magnitude 3.5 ligt qua helderheid halfweg magnitude 3 en 4. Om de overeenkomstige helderheidsverhouding te berekenen, nemen we de vierkantswortel uit 2.51188, dat is 1.585, dus we hebben: een ster van magnitude 3.5 is 1.6 keer zwakker dan een ster van magnitude 3, en 1.6 keer helderder dan een ster van magnitude 4.
De moderne magnitudenschaal wordt toegeschreven aan de Brit Robert Pogson.
In formulevorm kunnen we het verband tussen magnitudeverschillen en lichtkrachtverhoudingen als volgt uitdrukken.
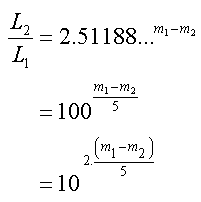
In het linkerlid staat L2 boven de breukstreep, in het rechterlid staat m2 daarentegen rechts van het minteken. Dat komt doordat kleine magnituden overeenkomen met grote helderheden, en grote magnituden met kleine helderheden.
We zouden de vorige formule graag omkeren: gegeven de helderheidsverhouding, hoeveel bedraagt dan het magnitudeverschil ?
Hiervoor moeten we de tweede omgekeerde bewerking van de machtsverheffing toepassen. De machtsverheffing is echter asymmetrisch (wiskundigen zeggen niet-commutatief) en heeft dus twee verschillende soorten omgekeerde bewerkingen. De ene is de worteltrekking. De andere, die we hier nodig hebben, is de logaritme.
Als a en b strikt positieve reële getallen zijn, dan noemen we de logaritme van b met grondtal a de macht waartoe we a moeten verheffen om b te bekomen. Dit getal noteren we alog b en het kan wiskundig worden aangetoond dat het gegarandeerd bestaat en uniek is. Het kan eventueel negatief zijn, of ook 0 (als b gelijk is aan 1).
2log 4 = 2
2log 8 = 3
8log 2 = 1/3
2log 0.5 = -1
10log 1000 = 3
10log 1000000 = 6
10log 10 = 1
10log 1 = 0
10log 0.1 = -1
10log 20 = 1.303...
10log 2.51188... = 0.4
Bij het rekenen met stermagnituden, en in heel wat andere toepassingen, wordt uitsluitend gebruik gemaakt van de logaritme met grondtal 10. In dat geval laten we meestal het grondtal weg, en schrijven simpelweg "log x" voor "de macht waartoe we 10 moeten verheffen om x te bekomen".
Uit de formule van de vorige paragraaf volgt nu
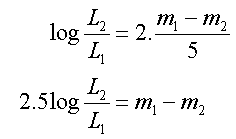
Deze laatste formule laat ons toe de fysische lichtkrachtverhouding te berekenen die bij een gegeven magnitudeverschil hoort.
Bovenstaande beschouwingen over de helderheid van sterren zeggen natuurlijk niets over de oorzaak waarom deze of gene ster helder of zwak aan de hemel prijkt: we spreken daarom wel van de schijnbare magnitude. De schijnbare helderheid van een ster wordt hoofdzakelijk beïnvloed door twee factoren: enerzijds de werkelijke hoeveelheid licht die ze uitstraalt, anderzijds de afstand tot de waarnemer.
Als twee sterren evenveel licht uitstralen, maar de eerste staat drie keer zo ver verwijderd als de tweede, dan zal ze ook zwakker schijnen, en wel met een factor die het kwadraat is van de verhouding der afstanden. Inderdaad, dezelfde hoeveelheid licht wordt verspreid over een oppervlak van een bol waarvan de straal drie keer zo groot is, dus de oppervlakte negen keer. In formulevorm luidt dit
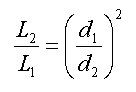
waar we d1 en d2 noteren voor de afstanden van de eerste respectievelijk de tweede ster tot de waarnemer, en L1 respectievelijk L2 voor hun schijnbare lichtsterkte. Let op de omgekeerde volgorde van de indices 1 en 2: hoe verder een ster, hoe zwakker ze lijkt.
De invloed van de afstand op de schijnbare magnitude bekomen we door de laatste twee formules te combineren:
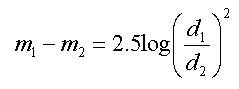
Uit de definitie van de logaritme volgt dat de logaritme van een kwadraat gelijk is aan het dubbele van de logaritme, dus
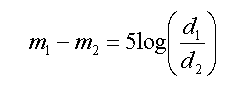
De absolute magnitude van een ster is de magnitude die ze zou hebben als we ze in gedachten verplaatsen tot op de standaardafstand van 10 parsec. Absolute magnitude wordt meestal met een hoofdletter M aangeduid, schijnbare magnitude met een kleine letter m. Als we de werkelijke afstand van de ster (in parsec) aanduiden met de letter d, dan volgt uit het voorgaande
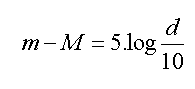
De zwakst bekende sterren hebben absolute magnitude 16 of 17. De helderste stralers halen ongeveer -7.
Opmerking. Er bestaat een vergelijkbaar begrip "absolute magnitude" voor planeten, kometen en andere objecten binnen het zonnestelsel. Daarvoor wordt echter als standaardafstand 1 astronomische eenheid i.p.v. 10 parsec genomen.
1. De ster van Barnard heeft schijnbare magnitude 9.54 en een parallax van 0.54901 seconden. We berekenen haar absolute magnitude door gebruik te maken van de formule d = 1/p en door de eigenschap dat de logaritme van het omgekeerde gelijk is aan het tegengestelde van de logaritme:
De absolute magnitude M bedraagt dus 13.24. Dit is een beetje uitzonderlijk, omdat deze ster zo dichtbij staat. De meeste sterren staan verder dan 10 pc van ons verwijderd, zodat hun absolute magnitude eerder kleiner is dan de schijnbare magnitude.
2. De schijnbare magnitude van de Zon bedraagt -26.73. Om haar absolute magnitude te berekenen, gebruiken we het feit dat 1 pc = 206265 AE:
| M | = | m - 5 log d + 5 |
| = | -26.73 - 5 log(1/206265) + 5 | |
| = | 4.84 |
Hiermee is de Zon een gemiddelde ster.
1. Bereken de absolute magnitude van Rigel (Bèta Orionis). Haar schijnbare magnitude bedraagt 0.18 en haar parallax (volgens Hipparcos) is 0.00422".
2. Uit statistisch onderzoek van de sterren in de bolvormige sterrenhoop M13 in het sterrenbeeld Hercules blijkt dat het verschil tussen de schijnbare en de absolute magnituden van deze sterren 14.33 bedraagt. Hoe ver staat M13 dan ?
Het verschil m - M is onafhankelijk van de eigenschappen van de ster, en hangt alleen af van haar afstand tot de waarnemer. Het wordt daarom de afstandsmodulus genoemd.
De schijnbare helderheid van een ster kan op verschillende manieren gemeten worden. Enkele veelgebruikte methoden zijn:
Deze verschillende meetmethoden zullen echter soms tegenstrijdige resultaten geven, in de zin dat een ster nu eens helderder, dan weer zwakker schijnt te zijn dan een andere ster. Dat heeft vooral te maken met verschillen in kleurgevoeligheid. Sterlicht is een mengeling van verschillende kleuren, in uiteenlopende verhoudingen.
We illustreren dit met de eerste twee meetmethoden (visueel en fotografisch). Klassieke fotografische materialen (bijvoorbeeld zilverchloride, AgCl) zijn vooral gevoelig voor blauw en violet licht, en weinig of niet voor rood licht. Vandaar dat vroeger in de donkere kamer een rood lampje mocht branden tijdens het ontwikkelen van een film. Rode voorwerpen lijken op oude zwartwitfoto's erg donker.
Als een ster vooral rood licht uitstraalt, zoals Betelgeuze (Alfa Orionis), dan lijkt ze misschien helder voor een menselijke waarnemer, maar zwak op een foto. Sterren die meer blauw licht afgeven, zoals Rigel (Beta Orionis), lijken juist erg helder op een foto.
Astronomen lossen dit probleem op door aan elk object verschillende magnituden mee te geven naargelang van de meetmethode. Zo spreekt men ondermeer van de visuele magnitude mv en de fotografische magnitude mpg. De bolometrische magnitude mbol meet het totale uitgestraalde vermogen in alle kleuren, inclusief de onzichtbare infrarode en ultraviolette straling. Ze is dus de meest "objectieve" maat, maar daar staat tegenover dat ze tamelijk moeilijk rechtstreeks te meten is.
Het verschil k = mpg - mv noemt men de kleurindex van de ster. Het is een positief getal voor oranje en rode sterren, en een negatief getal voor blauwe sterren.
Informatie over de verdeling van het licht van een ster over de verschillende kleuren is een erg belangrijk gegeven bij de fysische studie van de ster. Men heeft daarom het systeem verfijnd door niet twee, maar drie of meer verschillende metingen van de helderheid van de ster uit te voeren. Bij elke meting wordt een ander kleurfilter voor de telescoop geplaatst. Enkele bekende systemen van kleurmeting zijn:
De kleur van een ster is indicatief voor haar oppervlaktetemperatuur. Rode sterren zijn relatief koel (3000 graden), blauwe sterren erg heet (15000-30000 graden).
Uiteraard kan hetzelfde verhaal gehouden worden over absolute magnituden. Het verschil tussen schijnbare en absolute magnitude, de afstandsmodulus, is trouwens onafhankelijk van de kleur.
De kleurindices zijn dan weer onafhankelijk van de afstand, en dus dezelfde voor absolute of schijnbare magnituden.
De volgende tabel geeft de fotografische en de visuele magnitude van enkele bekende sterren. Bereken hun kleurindex en probeer daaruit hun kleur af te leiden.
| Populaire naam | Bayer | mpg | mpv | k | kleur |
|---|---|---|---|---|---|
| Spica | Alfa Virginis | 0.74 | 0.97 | ||
| Sirius | Alfa Canis Majoris | -1.47 | -1.46 | ||
| Antares | Alfa Scorpii | 2.77 | 0.94 |
Ook de "visuele" magnituden in deze tabel zijn fotografisch bepaald, door een geschikt kleurfilter voor de telescoop te plaatsten. Men spreekt in dat verband van de fotovisuele magnitude mpv
De bolometrische correctie BC mbol - mv bepaalt het gedeelte van het sterrenlicht dat onzichtbaar is voor het menselijke oog. Ze is steeds kleiner dan of gelijk aan nul. Ze is ongeveer nul voor witte sterren, en sterk negatief voor erg hete (blauwe) en erg koele (rode) sterren. De eerste soort zendt namelijk nogal wat ultraviolet licht uit, de tweede soort straalt een groot deel van zijn licht in het onzichtbare infrarood uit.
De kwaliteit van een telescoop wordt vooral bepaald door de hoeveelheid licht die hij verzamelt. Bij een goed instrument is die evenredig met de oppervlakte van de objectieflens (bij een refractor) of de hoofdspiegel (bij een spiegeltelescoop).
Door deze oppervlakte te vergelijken met die van een gemiddeld menselijk oog in het donker (circa 8 mm) kunnen we een schatting van de magnitudewinst maken. Als we ervan uitgaan dat het menselijk oog in goede omstandigheden sterren tot schijnbare magnitude 6 kan waarnemen, dan is de theoretische grensmagnitude van de telescoop
mgrens = 6 + 5.log (diameter/8)
waarbij de diameter van het objectief in millimeter wordt uitgedrukt. In werkelijkheid wordt deze limiet bijna nooit gehaald, omdat waarnemen door een telescoop minder comfortabel is dan met het blote oog, en omdat in het instrument een deel van het licht verloren gaat.
Als een binoculair het opschrift "7 x 50" draagt, dan betekent dat een vergroting van 7 keer en een lensdiameter van twee keer 50 mm. Met een dergelijk instrument zijn theoretisch nog sterren zichtbaar van magnitude 6+5.log(50/8)=10.
Bepaal de theoretische grensmagnitude van een Kuttertelescoop waarvan de hoofdspiegel 25 cm doormeter heeft.