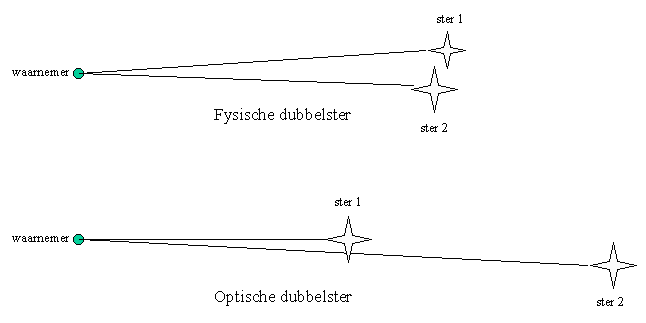
Vaak blijken sterren in paren aan de hemel te staan. In sommige gevallen is dat een toevallige samenstand, terwijl de twee sterren in werkelijkheid heel verschillende afstanden van ons verwijderd zijn: we spreken dan van optische dubbelsterren. Als de sterren werkelijk relatief dicht bij elkaar staan, vormen ze een fysische dubbelster. In dat geval zullen de de sterren onder invloed van elkaars zwaartekracht een cirkel- of ellipsbaan om elkaar heen beschrijven, net zoals de planeten banen beschrijven rond de Zon.

Een voorbeeld van een optische dubbelster is alfa Cas (Shedir, modern Arabisch sadr, borst). Deze heldere oranje ster (K0) heeft een blauwe buurvrouw van magnitude 9.
In het vervolg van deze tekst hebben we het uitsluitend over fysische dubbelsterren. De eerste baanbeweging, en daarmee ook het eerste bewijs van het bestaan van fysische dubbelsterren, werd vastgesteld bij alfa Gem (Castor) door William Herschel in 1804. Hij was eigenlijk op zoek naar een optische dubbelster, om parallaxverschillen te meten !
Naast dubbelsterren bestaan er ook driedubbelsterren en zelfs meervoudige stersystemen van 4, 5 of 6 componenten. Uit statistische onderzoeken blijkt dat de meerderheid van de sterren tot een meervoudig stersysteem zou behoren, al is dit vaak moeilijk waarneembaar wegens de geringe onderlinge afstand van de componenten.
Ook het zonnestelsel kan met een beetje goede wil als een dubbelster worden opgevat: Jupiter zendt meer straling uit dan hij ontvangt, en is dus in feite een "mislukte" ster.
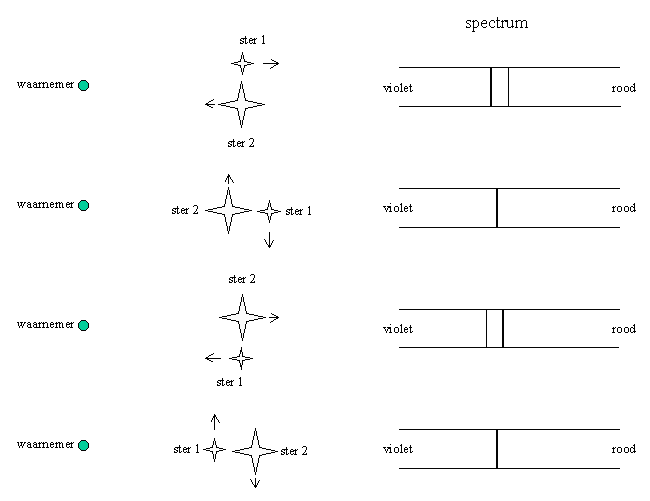
Om nauwe dubbelsterren te ontdekken komt de studie van sterspectra van pas. Als gevolg van de onderlinge omwenteling van de componenten, hebben ze meestal verschillende radiële snelheden. Dit verraadt zich in het spectrum als een periodieke verdubbeling en ontdubbeling van de absorptielijnen.
Door nauwkeurige studie van de periodieke verschuiving van de absorptielijnen kan reeds heel wat worden afgeleid over de baan van de dubbelster. Dubbelsterren waarvan het meervoudige karakter uitsluitend uit het spectrum af te leiden valt, noemen we spectroscopische dubbelsterren.
In enkele uitzonderlijke gevallen schuift één van de twee componenten periodiek voor de andere, waardoor een tijdelijke verzwakking van de totale helderheid optreedt. Amateurs van veranderlijke sterren noemen dit bedekkingsveranderlijken, wij spreken in dit hoofdstuk van eclipsdubbelsterren.
Bij sommige dubbelsterren is één van de twee componenten volkomen onzichtbaar, en blijkt het dubbele karakter slechts uit positieschommelingen van de andere (zichtbare) ster. Omdat de ontdekking van dergelijke dubbelsterren nauwkeurige positiemetingen vergt, noemt men dit astrometrische dubbelsterren. Sirius B, de begeleider van de heldere ster alfa CMa, was reeds astrometrisch bekend voor hij rechtstreeks werd waargenomen.
Bij zijn pogingen om de bewegingen der planeten te verklaren, ontdekte Johann Kepler een merkwaardig verband tussen enerzijds de gemiddelde afstand van een planeet tot de zon, anderzijds haar omwentelingstijd.
Drukken we even de afstanden uit in Astronomische Eenheden (1 AE = gemiddelde afstand Aarde-Zon = 150 miljoen km), en de omwentelingen in jaren (= omwentelingen van de Aarde om de Zon), dan krijgen we de volgende tabel:
Mercurius Venus Aarde Mars Jupiter Saturnus
omwenteling 0.24 0.61 1.00 1.88 11.9 29.5
afstand 0.39 0.72 1.00 1.52 5.20 9.54
Kepler berekende de kwadraten van de omwentelingstijden (d.i., de omwentelingstijd vermenigvuldigd met zichzelf) en de derdemachten van de afstanden (d.i., de afstand tweemaal vermenigvuldigd met zichzelf). Hij bekwam de volgende merkwaardige resultaten:
Mercurius Venus Aarde Mars Jupiter Saturnus
kwadr.omw. 0.058 0.37 1.00 3.53 142 870
derdem.afst. 0.059 0.37 1.00 3.51 140 868
Deze getallen zijn nagenoeg gelijk ! (De kleine verschillen zijn te wijten aan afrondingsfouten). Als we natuurlijk de omwentelingstijd en de afstand in andere eenheden uitdrukken, bijvoorbeeld in dagen resp. kilometer, dan zijn de beide getallenrijen niet meer gelijk, maar toch nog evenredig. De evenredigheidsfactor bedraagt dan
Kepler formuleerde dit als de derde van zijn drie wetten die de planeetbanen beschrijven:
De kwadraten van de omlooptijden verhouden zich als de derdemachten van de gemiddelde afstanden tot de Zon.
Isaac Newton slaagde er later in de wetten van Kepler als bijzondere gevallen af te leiden uit zijn algemene wetten van de mechanica en zijn wet van de zwaartekracht. Daaruit volgde dan verder nog dat de evenredigheidsfactor te maken heeft (evenredig is) met de massa van de Zon.
De derde wet van Kepler geldt ook voor andere "planetenstelsels".
Zo hebben we de volgende gegevens voor de vier grootste manen
van Jupiter (bron:
http://ssd.jpl.nasa.gov/sat_elem.html).
Io Europa Ganymedes Callisto
omwenteling (dagen) 421800 671100 1070400 1882800
afstand (km) 1.769 3.551 7.155 16.689
De verhouding tussen de derdemacht van de afstand en het kwadraat van de omlooptijd bedraagt bij allevier de manen: 2.40 x 1016 km3/dag2. Dat is een goede 1000 keer minder dan hierboven bij de planeten van het zonnestelsel. De massa van Jupiter bedraagt dan ook iets minder dan één duizendste van de massa van de Zon.
De Maan draait op ongeveer 384000 km van het centrum van de Aarde, en één maand duurt 27.3 dagen. Hoeveel keer lichter dan de Zon is de Aarde ?
Het verband dat Newton vond, kan eenvoudig gereconstrueerd worden door de middelpuntzoekende kracht van een éénparig cirkelvormige beweging gelijk te stellen aan de zwaartekracht:
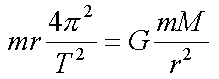
Hierin is
| m | de massa van de satelliet |
| M | de massa van het centrale lichaam |
| r | hun onderlinge afstand |
| T | de omlooptijd van de satelliet |
| G | de universele zwaartekrachtconstante 6.6726 x 10-11 kg-1m3s-2 |
Hieruit volgt dat de evenredigheidsconstante van de derde wet van Kepler, uitgedrukt in standaardeenheden (m3s-2) gegeven wordt door
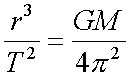
Bovenstaande formule wordt echter meestal omgekeerd gebruikt: men meet de omlooptijd en afstand van een satellietlichaam om daaruit de massa van het centrale lichaam te berekenen.
Bereken de massa van de Aarde uit de baangegevens van de Maan. Let op: gebruik de standaardeenheden meter en seconde !
Bij dubbelsterren kan deze berekening eveneens worden uitgevoerd, met de volgende twee aanpassingen:
Bereken de gezamenlijke massa van het stelsel Sirius AB (alfa CMa), gebruikmakend van de gegevens op het einde van de les Afstand van sterren en van het feit dat de omloopperiode van deze dubbelster 50 jaar bedraagt.
Een belangrijk probleem om met de derde wet van Kepler de massa van een dubbelsterpaar te berekenen, is dat de gemiddelde onderlinge afstand bekend moet zijn. Als de dubbelster ver weg staat, kunnen we haar parallax niet meten, en kennen we dus alleen de schijnbare onderlinge afstand in boogseconden. In de volgende paragraaf leggen we uit hoe hieraan verholpen werd door een belangrijke astrofysische ontkekking.

Arthur Eddington (later Sir Arthur) ontdekte in 1917 langs theoretische weg een verband tussen de massa van een ster en haar absolute bolometrische magnitude. Statistische verificatie leverde de volgende vergelijking
Anders gezegd, "de lichtkracht van een ster is evenredig met haar massa tot de macht 3.6".
Waar komt die constante 4.77 vandaan ?
Met de ontdekking van nucleaire energie en de verklaring van de energieproductie van sterren door kernfusie kwam nog verdere theoretische bevestiging van de massa-lichtkrachtrelatie van Eddington. Wel moest een verfijning worden aangebracht naargelang van het soort kernreacties dat de energieproductie domineert, naargelang van de massa van de ster:
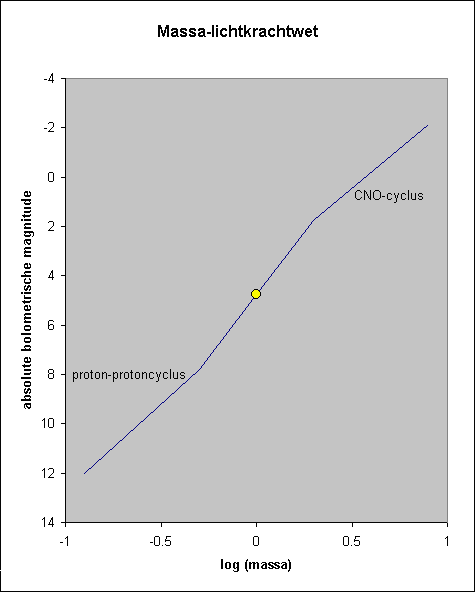
De massa-lichtkrachtwet gaat uit van stabiele waterstofverbranding in de ster, en is dus in principe slechts geldig voor hoofdreekssterren.
In al deze formules en getallen dreigt de volgende waarheid een beetje verloren te gaan: een relatief klein massaverschil veroorzaakt een enorm verschil in helderheid. De zwaarste hoofdreekssterren zijn niet meer dan een hondertal keren zwaarder dan de lichtste, maar ze zijn wel een miljoen keer zo helder ! Een gevolg hiervan is dat zware sterren veel sneller verouderen dan lichte sterren: hun iets grotere waterstofvoorraad geraakt onevenredig snel opgebrand.
Veronderstel nu dat we over nauwkeurige waarnemingen van de baanbeweging van een dubbelster beschikken, maar niet over de parallax (bijvoorbeeld, omdat de dubbelster te ver weg staat). We kennen dus niet de werkelijke gemiddelde afstand a tussen de componenten, maar wel de hoekboog s die ermee overeenkomt. Als a wordt uitgedrukt in astronomische eenheden, en s in boogseconden, dan is de parallax p (eveneens uitgedrukt in boogseconden) het quotiënt van s met a.
Anderzijds, als P de onderlinge omlooptijd in jaren is, dan zegt de derde wet van Kepler
waar massa_1 en massa_2 de massa's van de dubbelstercomponenten zijn, uitgedrukt in zonsmassa's.
De massa's van de componenten kennen we niet. We weten echter dat stermassa's niet dramatisch verschillen (we kijken niet op een factor 100), en dus maken we geen erge fout als we beide massa's eventjes gelijk aan die van de Zon veronderstellen. We krijgen dan een "benadering" van de parallax:
Maar met behulp van deze benaderde parallax kunnen we de absolute bolometrische magnituden van de twee componenten berekenen. Via de massa-lichtkrachtwet krijgen we dan een betere benadering van hun massa's.
Die massa's gebruiken we dan opnieuw om een betere benadering van de parallax de verkrijgen, enzovoort. Het mooie is, dat dit procédé na enige malen herhalen convergeert naar een welbepaalde waarde. De aldus berekende waarde van p noemt men de dynamische parallax van de dubbelster.
We doen alsof we de parallax van alfa Centauri niet kennen (in feite is die parallax behoorlijk groot en dus relatief nauwkeurig meetbaar). We nemen wel de volgende meetgegevens aan:
| mbol | -0.09 (component A) resp. +0.80 (component B) |
|---|---|
| omlooptijd | 79.9 jaar |
| scheiding | 17.58" |
We veronderstellen eerst massa_1 = massa_2 = 1. Dan is de parallax
Dit levert afstandsmodulus m - M = 5 log(d/10) = -4.38, dus de absolute bolometrische magnitudes zijn +4.29 en +5.18; volgens de massa-lichtkrachtwet krijgen we de gecorrigeerde massa's
| massa_1 | = | 1.12 |
| massa_2 | = | 0.91 |
Dit levert een gezamenlijke massa van 2.03 zonsmassa's, slechts een klein beetje meer dan aanvankelijk verondersteld. We corrigeren dus de parallax tot
De rechtsteeks gemeten parallax van alfa Centauri is overigens 0.751".
Bepaal de dynamische parallax van eta Cassiopeiae. De heldere component heeft schijnbare visuele magnitude 3.47 en is een G0-ster (bolometrische correctie -0.03), de zwakkere component heeft magnitude 7.22 en klasse M0 (BC = -1.20). De componenten draaien in 480 jaar om elkaar heen. De gemiddelde onderlinge afstand wordt gezien onder een hoek van 11.99". (Ter vergelijking: de rechtstreeks gemeten parallax is 0.176").